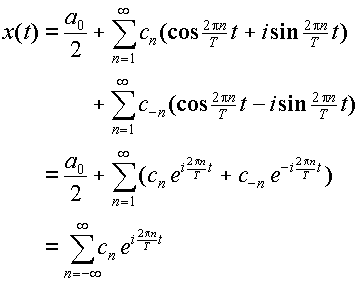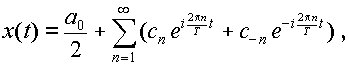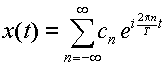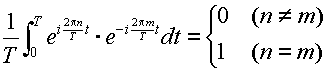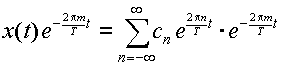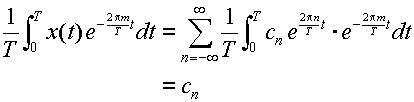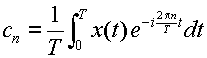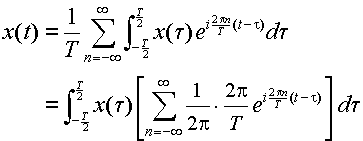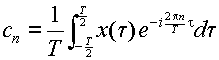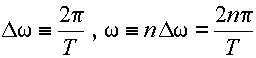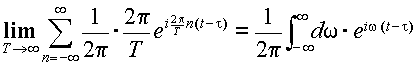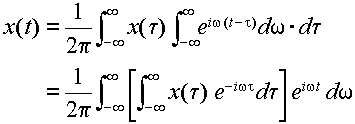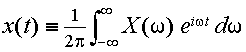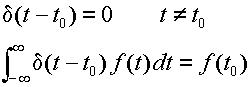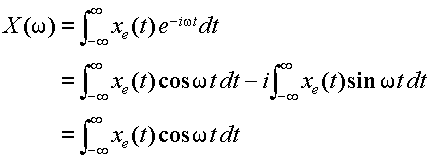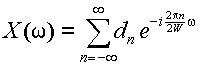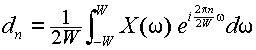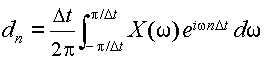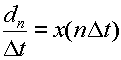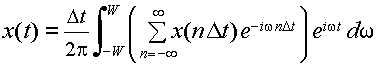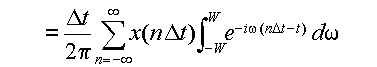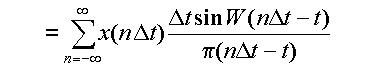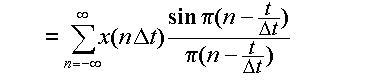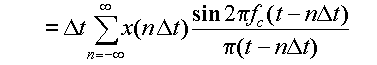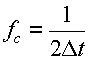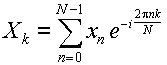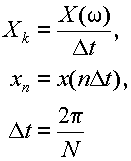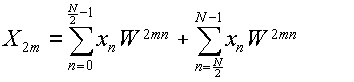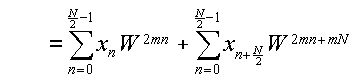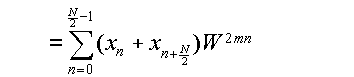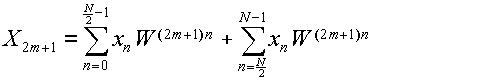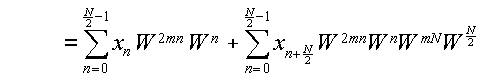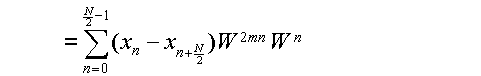オブジェクト指向スクリプト言語Rubyのための高速フーリエ変換拡張ライブラリ, 「NumRu/fftライブラリ」を製作した.その発端となったdennou-rubyプロジェクトは,dennou-davisプロジェクトのサブプロジェクトとして地球惑星流体物理学におけるデータ分析,ビジュアル化,および数値シミュレーションを促進する一連の汎用ソフトウェアの開発を目標としている研究グループである.オブジェクト指向スクリプト言語Rubyは,開発効率,拡張性,可搬性の観点から,「クリック一発で絵が描ける数値データ」の構築を目指すdennou-davisプロジェクトの目的に適ったプログラミング言語である.
　NumRu/fftライブラリは,FFTW,もしくはISPACKを内部で呼び,C言語のライブラリとRubyのインタフェースの仲立ちをするラッパライブラリである.入出力にはNArrayクラスを用いている.NumRu/fftライブラリを使用する際は予めこれらのライブラリをインストールしておく必要がある. NumRu/fftライブラリは未だ拡張の余地があり,今後も開発を続けていくものである.
URL: http://www.ep.sci.hokudai.ac.jp/~kazto/work/

　筆者が製作したオブジェクト指向スクリプト言語Rubyのための高速フーリエ変換ライブラリ, 「NumRu/fft」を紹介する.

　本論文は二本の柱からなっている.ひとつは,フーリエ変換とその離散化,高速フーリエ変換のアルゴリズムについての議論である.まずはじめに,そもそもフーリエ変換とはいかなるものかを振りかえるために,フーリエ級数から議論する.フーリエ級数からその拡張としてフーリエ積分変換を導出し,さらにそれを数値計算になじむように離散化をするための導出を行う.そして,高速フーリエ変換のアルゴリズムについて議論する.もうひとつの柱は,オブジェクト指向スクリプト言語Rubyについての解説である.

　高速フーリエ変換の計算方法は, Cooley,J.W., and J.W.Tukey (1965)^[1]が最も有名である.当時,IBM Yorktown Heights Research Center のガーウィン(R.L. Garwin)は,自身の研究のためにフーリエ変換の高速な計算方法を探索しており,フーリエ変換についての論文を書きつつあったチューキーに対して何か良い手法が無いかと尋ねた.このときにチューキーが説明したものが,クーリー・チューキーの計算法と後々呼ばれる事となる方法の元となる考えかたであった.ガーウィンはIBM研究所にチューキーが説明した方法をプログラム化することを依頼した.この時に要請を受け入れたのが,クーリーであった.クーリー自身はこのプログラミングの仕事を一時のものと考えていたが,次第にこのプログラムに対する賞賛の声や,プログラムのコピーの要求が増えてゆき,1965年,クーリーとチューキーはこの計算法についての論文を発表するに至る.

　私はもともとRubyを用いたプログラミングに興味があり,常々Rubyに対して貢献したいと考えていた.そのような折にdennou-rubyプロジェクトを紹介され,Rubyにおいて高速フーリエ変換を行うライブラリの必要性について話を伺った.そこで,ライブラリ作成の作業を是非やらせて欲しいと志願した次第である.dennou-rubyプロジェクトについて,次節で詳しく解説する.次節および第4章において,Rubyがdennou-rubyプロジェクトの目的に最適なプログラミング言語であることをRubyの特徴を列記しつつ示す.その特徴であるところのオブジェクト指向の考え方,および拡張ライブラリの特徴について言及する.

　最後に,Rubyにおける多次元配列ライブラリNArrayのために既存の高速フーリエ変換ライブラリを利用する事を可能にする,拙作ラッパライブラリ「NumRu/fft」について紹介する.なお,本論文^[19]はWWWからも閲覧可能である.NumRu/fftライブラリのダウンロード先^[20].共々,参照されたい.

　dennou-rubyプロジェクト^[11]は,地球惑星流体物理学におけるデータ分析,ビジュアル化,および数値シミュレーションを促進する一連の汎用ソフトウェアの開発を目標としている研究グループである.プロジェクトが提供するものはオールインワンで実行できるプログラムでは無く,オブジェクト指向スクリプト言語Rubyにおいてプログラミングする際に用いるための,ライブラリの集合体である.

　科学的な研究の手法は非常に多岐にわたっているので,それら一つひとつのニーズをマウスで操作するようなグラフィカル・ユーザ・インタフェースの環境において満足させることは困難である.研究者は,大なり小なりのプログラミングを行う必要に迫られるであろう.プログラムを記述することによって,研究者が意図する作業を意図した通りに行う事ができ,さらに,必要ならば同じ作業を容易に任意回数くり返すことが可能となる.もちろんこれらの作業は多くの研究者,および学生が長い間行ってきた作業である.しかしながら,その効率は使用するプログラミング言語に強く依存する.プログラミング言語によって使用する事のできるライブラリの種類が違ってくるためである.

　オブジェクト指向スクリプト言語Rubyは,科学的研究を行う上での多くの観点から最良の環境を提供するような特徴を持っている.詳しくは第4章に述べる.さらに,Rubyは研究作業を容易にするだけでなく,従来の言語よりも研究者同士の間で,データ,プログラム,ソフトウェアなどの研究成果を共有することを容易にする.これにより, Rubyを実行する環境を整えさえすれば,迅速に研究作業に取りかかる事が可能となる.

　そもそもdennou-rubyプロジェクトは,dennou-davisプロジェクトのサブプロジェクトである.地球流体電脳倶楽部によると,dennou-davisプロジェクトとは,「クリック一発で絵が描ける数値データ」を合い言葉に,地球および惑星にまつわる流体現象を念頭においた多次元数値データの構造化と可視化を研究し,研究教育資源の開発を目指す有志の研究グループである.しかし,実際に「クリック一発」でデータを処理するには地球流体科学で扱われるデータはあまりに大規模であり,また多様でもある.それらの膨大かつ多様なデータを処理するための速度が,研究を行うに際してボトルネックとなっているのが現状である.これを改善する為には,業界標準となるデータ構造とそれに対応したデータ処理の手法が必要となってくる.dennou-davisプロジェクトは,機種,OSに依存しない,ネットワーク透過性に優れている,自己記述的なデータ構造などの観点から標準データ構造としてNetCDF^[12]を採用し,また,そのデータを処理するための方法として数値処理に特化したFORTRAN90,そして自己記述データと親和性の高いオブジェクト指向プログラミングが可能なRubyの二つのアプローチを採択している.dennou-rubyプロジェクトの製品として,RubyでNetCDFのデータを扱うインタフェースライブラリ「RubyNetCDF」^[16],地球流体電脳倶楽部の製品である,FORTRANによる可視化ライブラリ「DCL」^[15]をRubyでも扱えるようにするラッパライブラリ「RubyDCL」^[17],「AdvancedDCL」^[18]などがある.

　フーリエ級数(Fourier Series)は, 有限区間 0≦t≦T で定義された関数,あるいは周期がTの周期関数を次のように正弦級数と余弦級数で展開して表わしたものとして定義される。

(3.1.1)

この式が成り立つための条件は,x(t) がたかだか有限個の有限な不連続点しか持たず,また,あっても有限個の極値,極大値, または極小値を持つことである.これを,ディリクレの条件と言う.

　(3.1.1)式は, 係数 a_n 及び b_n を以下のようにおきかえる事で,より簡単な形で表わす事ができる.

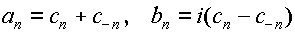(3.1.2)

を代入すると,

	(3.1.3)
	(3.1.4)
	(3.1.5)

となる.ただし,

(3.1.6)

とした.

　次の式は,直交関係の式として有名であり、容易に証明できる.

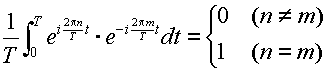(3.1.7)

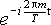
式(3.1.5)の両辺に をかけて式(3.1.7)を用いると,

	(3.1.8)
	(3.1.9)
	(3.1.10)

を得る.式(3.1.2)を用いて書き換えれば,

	(3.1.11a)
	(3.1.11b)

を得る.

　前節に示したフーリエ級数は,有限区間[0,T]で定義された関数,もしくは周期Tの周期関数についてのみ適用する事ができる.ここでは,より一般的な関数,非周期的関数にまでフーリエ級数を拡張する.この拡張は,非周期的関数の周期は,T→∞の極限を考えることで実現できる.

　前節では有限区間を [0,T] としたが,ここでは [-T/2,T/2] ととる.この時のフーリエ級数は次のように与えられる.

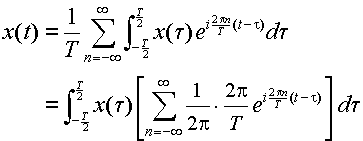	(3.2.1)
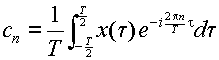	(3.2.2)

式(3.2.2)を式(3.2.1)に代入すると,

	(3.2.3)
	(3.2.4)

T→∞とし,

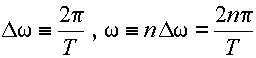(3.2.5)

とおくと,[ ] で囲んだ部分について積分におきかえる事ができる.

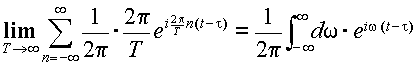(3.2.6)

よって,

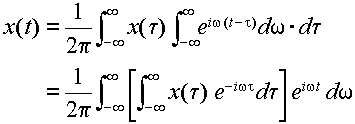(3.2.7)

ここで,式(3.2.7)の [ ] の部分を

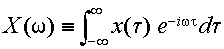(3.2.8)

とした時,このＸ(ω)を x(t) のフーリエ変換と呼ぶ.また,式(3.2.7)をX(ω)で表わすと,

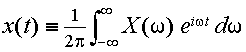(3.2.9)

となり,これはフーリエ逆変換を表わしている.

　次に,インパルス関数に対するフーリエ変換について議論する. ここでは,インパルス関数を次のようなある関数に対して数値 f (x) を割り当てるような超関数として定義する.

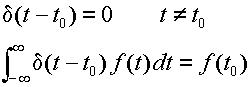(3.2.10)

この関数は,ディラック(Dirac)のδ関数と呼ばれる.このインパルス関数δ(t) に対してフーリエ積分を行なう. ここで t₀=0 としても一般性を失わないので,

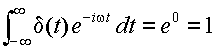(3.2.11)

を得る.

　式(3.2.9)のx(t)が実数関数であり,偶関数,もしくは奇関数であった場合,フーリエ変換は特別な形に書きかえる事ができる.まずは,x(t)=x_e(t),偶関数の場合を考える.このとき,フーリエ変換公式,式(3.2.8)は次のように書きかえられる.

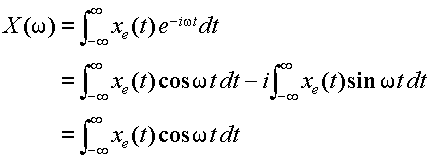(3.3.1)

式(3.3.1)の2行目第2項は,非積分関数は奇関数となるので0に等しい事を用いた.この形で表わしたものを,フーリエコサイン変換と呼ぶ.このときのX(ω)もまた,X(-ω)を計算することで偶関数であることが容易に導出できる.

　次に,x(t)=x_o(t),奇関数の場合を考える.同様にして式(3.2.8)を書きかえると,

(3.3.2)

となり,Ｘ(ω)は純虚数の関数として表わされる.このＸ(ω)に含まれる虚数iを外に出した形にした

(3.3.3)

を,フーリエサイン変換と呼ぶ.これもコサイン変換同様,Ｘ'(-ω)を計算すると,-Ｘ'(ω)になり,奇関数である事がわかる.

　この節では,先に述べた連続的な関数のフーリエ変換を,計算機上で行なうことを可能にする為に適当な修正を行なう. すなわち,連続な関数を離散的な数列に変換する「標本化(sampling)」と,定義域を有限にする「局所化」である.

　ある関数 x (t) のフーリエ変換 X(ω) が局所的であるとする.すなわち,あるWに対して

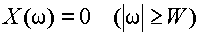(3.4.1)

を満足していると仮定する.

　X(ω)が周期 2W の周期関数であると見なすと,フーリエ級数が次のように計算できる.

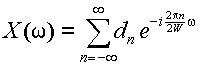	(3.4.2)
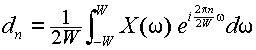	(3.4.3)

式(3.4.2)では,式(3.2.10)とは異なり,i の代わりに-i とおいた.フーリエ変換の逆変換の式,式(3.2.11)

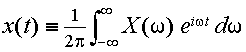(3.4.4)

と比較する為,式(3.4.3)をπ/W = T とおきかえると,

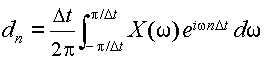(3.4.5)

と書ける.式(3.4.1)の条件より,式(3.4.5)の積分区間は-∞から∞までと考えてよいので,式(3.4.4)と比較して,

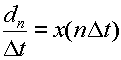(3.4.6)

となる.これを式(3.4.2)に代入すると

(3.4.7)

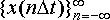
となる.この式はX(ω)のフーリエ係数d_nがx(t)を間隔Tごとにサンプルした標本値系列であることを示している.

　再びフーリエ逆変換の式,式(3.2.9)を用いると,

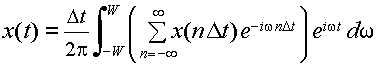	(3.4.8a)
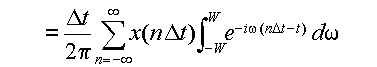	(3.4.8b)
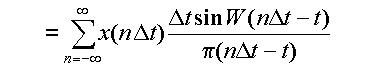	(3.4.8c)
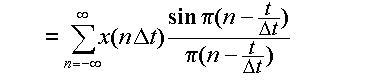	(3.4.8d)
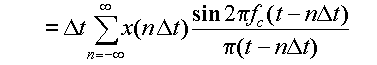	(3.4.8e)

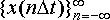
となる.これは,間隔Tごとに標本化したx(t)の値 から,もとの関数 x(t) を再現できることを示している.

　この時のTは,標本化した際のt座標の間隔であるが,これを

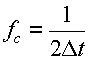(3.4.9)

と表わしたとき,1/2T=f_cを「ナイキストの標本化周波数(Nyquist sampling rate)」(あるいは単にナイキスト周波数)と言う.もし間隔Tで標本化した連続関数 x(t) の周波数帯域がf_cより小さい周波数に限られていたなら,関数 x(t) は標本 x_n から完全に再現されうる.逆に,帯域幅がナイキスト周波数を越えてしまうような連続関数を標本化する時には, -f_c < f < f_cの範囲外のフーリエ変換の結果が帯域幅の内側にひずみとして現れてしまう.この現象をエイリアシング(aliasing, または折り返しひずみ)という.

　ここでは,はじめに周波数領域の関数X(ω)が限られている(局所的である)と仮定したが,逆に時間領域の関数x(t)が有限区間で定義されている(局所的である)とした場合でも,同様の結果が得られる.即ち,周波数を局所的にすれば時間に離散化とサンプリング定理が適用され,時間を局所的にすれば周波数に離散化とサンプリング定理が適用される.　

　離散フーリエ変換を計算するにはN²回の乗算が必要であり, N が大きくなると計算に必要な時間は急速に増大する.ところが,1965年にクーリーとチューキーによって提案された高速フーリエ変換(Fast Fourier Transform, 略して FFT)のアルゴリズムは,これを最小で N logN回にまで減らす.この節では,FFTの数学的側面を簡単に述べる.

　式(3.4.7)は,次のように書きかえる事ができる.

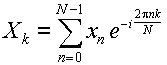(3.5.1)

これは,

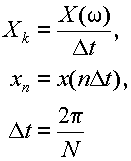(3.5.2)

としたものである.式(3.5.1)はさらに書きかえる事ができて,

(3.5.3)

とできる.

　Nが偶数である場合を考える.k=2m,即ちＸ_kの偶数番目の成分に注目したとき, Ｗ^N=1である事を利用して,

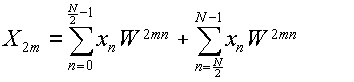	(3.5.4a)
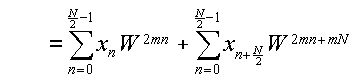	(3.5.4b)
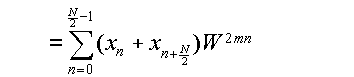	(3.5.4c)

と表わせる.この時,

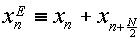(3.5.5)

とおくなら,式(3.5.4)は,Ｘ_2m(m=0,…,N/2-1)が長さN/2の数列 x'_nのフーリエ変換となる事を表わしている.

　同様にして,k=2m+1,即ちＸ_kの奇数番目の成分に注目したとき,Ｗ^N/2= -1となる事を利用して,

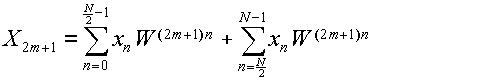	(3.5.6a)
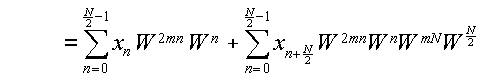	(3.5.6b)
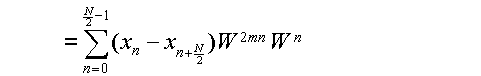	(3.5.6c)

と表わす事ができる.式(3.5.5)同様,

(3.5.7)

とおくと,式(3.5.6)はＸ_2m+1(m=0,…,N/2-1)が長さN/2の数列 x''_nのフーリエ変換となる事を表わしている.

　この分割を,2で割り切れる段階まで進めることで計算回数を減らしていく事ができる.N=2^Mで表わせる場合が最も効率良く,あるひとつのＸについての和の計算がlogN=M回,数列Ｘすべてについては,NlogN回の計算で結果を得る事ができる.以上が高速フーリエ変換のアルゴリズムである.

　オブジェクト指向スクリプト言語「Ruby」は,1993年,まつもとゆきひろ氏を中心とする,有志数名によって作られた.Rubyには,以下のような特徴がある.Perlに匹敵する文字列処理能力などの一般的な特徴はここでは省き,計算惑星科学にとって重要であるものをここに挙げる.

• 他の言語とは異なり,徹底したオブジェクト指向の思想のもとに設計されたインタプリタ言語
• シンプルな文法
• ガベッジコレクタ(GC)機能
• イテレータ
• 対話的にスクリプトを実行することで試行錯誤とデバッグを容易にするインタフェースの存在
• UNIXをはじめ,Windows,Macintosh上でも動作する,高い移植性
• GPL(GNU Public License)に基づく,オープンソースのフリーソフトウェア
• 拡張ライブラリをC言語で記述する事によるグルー性の高さとボトルネックの改善
• 製作者が日本人

　オブジェクト指向言語であること,シンプルな文法,GC,ループを抽象化する「イテレータ」の存在,対話インタフェースの存在などの要因は,すべてプログラミングを容易にしている.これは,プログラミング作業そのものに煩わされること無く研究本体に専念する事を可能にし,開発効率を向上させることを意味している.また,RubyはもともとUNIX環境で製作されたプログラミング言語であるが,設計段階でプラットフォームに依存しない実行環境を目指して製作されているので,ひとつのスクリプトを数多くのUNIX系OSはもちろん,WindowsやMacintoshなどのOS上でも同様に実行する事ができる.この様なプログラミング言語がGPLに従って無償で配布されていることも,導入を容易にするという点においてRubyの可搬性を優れたものとしている.

　つぎに,他のプログラミング言語と比較した際のRubyの利点について述べる.科学計算においては, C, FORTRAN77, 数値計算やグラフィックの為のライブラリを備えたFORTRAN90などがよく用いられるが,いずれもコンパイラ言語であり,試行錯誤の段階でのコンパイル作業は時間のロスが大きい.コンパイラ言語はアプリケーション開発者の為のもので,エンドユーザが用いるには手間が多すぎるといえる.

　また,大気科学,及び海洋学などの分野においてよく用いられるアプリケーションとして,GrADSが挙げられる.これは,データを単なる多次元の配列としてではなく,単位と座標を持った,自己記述的な物理量として扱い,これによってデータ解析を迅速かつ容易に行う事ができる.しかしGrADSでは扱うデータのタイプが限られており,ユーザの欲求を必ずしも満たすものではない.また,GrADSはプログラミング言語として完全ではないので,カスタマイズ性と自動化の面に難がある.

　さらには,対話的に使用する事のできるプログラミング言語として, IDL, Matlab (そのクローンとしてOctave), yorick などがある. IDL, Matlab は商用プログラミング言語であり,広範囲なグラフィック機能と数学ライブラリを備えている.これらは,今までの中では最良の選択であったかもしれないが,それでもいくつかの欠点が存在する.一つ目は,これらの言語はオブジェクト指向言語ではない事である.すなわち,これらの言語は柔軟性に欠け,汎用アプリケーションを開発する目的には向かない事を意味している.例えば,ファイルフォーマットによらないようにデータの扱いを統一する事は困難な作業となるであろう.IDLの最近のバージョンではオブジェクト指向の特徴が組みこまれてはいるものの,実用的ではない.二つ目の欠点として挙げられるのは,何より IDL や Matlab はフリーのソフトウェアではないと言う事である. Octaveやyorickはフリーソフトウェアであるものの,機能的には十分ではない.また,使用する事のできるプラットフォームが制限される.これらの言語はスーパーコンピュータにおいては対応されていない限り使用する事ができない.三つ目は,Cなどの他の言語によって言語を拡張する事が難しいと言う事である.商用ソフトウェアであり,ソースコードが公開されていない点もユーザによる拡張を妨げる要因となっている.この点に関しては,Rubyは奇跡的とも言えるほどにC言語による拡張性が高い.本論文で紹介している NumRu/fft ライブラリも,この特徴の賜物といえる.

　この節では,オブジェクト指向という方法論について簡単に説明する.オブジェクト指向とは,最も簡単に要約するなら,その名の示す通り「オブジェクトを中心にした考え方」である.より詳しく表現するなら,次の三つの概念に象徴されている.

• カプセル化 (情報隠蔽)
• ポリモーフィズム (多態性,動的結合)
• 継承

　カプセル化とは,あるデータと,それに対する手続きを一体化し,あるデータへのアクセスを決められた手続きだけに限定して行うようにする事である.これにより,ある関数について入力と出力さえ把握していれば,関数の中で何が行われているかを気にする必要がなくなる.それを実現するのが,クラスという考えかたである.クラスとは,あるオブジェクトについて特徴を抽象化し,一つのグループとしてまとめたものである.つまり,オブジェクトをクラスにまとめる事がカプセル化と同義とも言える.Rubyでは,すべてのデータがオブジェクトとして扱われていて,オブジェクトの内部の状態がメソッドを経由する以外の方法では外部からアクセスする事ができないことにより,カプセル化を実現している.

　ポリモーフィズムとは,多態性とも言い,「オブジェクトは,己がどう振る舞うべきかを知っている」という言葉に象徴されている.例えばRubyには,文字列 str = "abcdef" があったときにその文字列の長さを知りたい時は「length」というメソッドが存在していて,つぎのように実行する.

ruby> str = "abcdef"
ruby> print str.length
6

また,配列 ary = [1,2,3,4,5,6] があったときに配列の長さを知りたい時にも,「length」メソッドが用いられる.

ruby> ary = [1,2,3,4,5,6]
ruby> print ary.length
6

内部的には文字列の長さを調べる行為と配列の長さを調べる行為は異なっている.しかしそれぞれのオブジェクトに対して「length」(長さを知りたい)というメッセージを送った時に,それぞれのクラス内で定義されている適切なメソッドを選んで実行している.実際に作業を始める段階になってから,対象となるオブジェクトに応じてどの具体的な手続きを適用するか決定されるので,動的結合と呼ばれる事もある.ポリモーフィズムによって,例えば,この「length」と言うメッセージが新しいクラスに対応しなければならないとき,新しいクラスの側を正しく定義すれば,メッセージを送る側のルーチンを一切書きかえる必要なしに,「length」ルーチンを拡張する事ができる.

　最後に継承について述べる.これは,ある雛型となるクラス(スーパークラスと言う)から,少しだけ特徴の異なる新しいクラス(サブクラスと言う)を定義することを指す.クラスがデータと手続きの集合体であることを思い出せば,クラスを継承することによって資源を節約しつつ,効率と見通しの良いプログラミングが可能となると言える.例を用いて説明すると,「柴犬」というクラスがあったとき,この柴犬クラスは「犬」というスーパークラスを継承している、と言う事ができる.同様に,「チワワ」クラスも,「犬」スーパークラスのサブクラスと言える.「柴犬」クラスと「チワワ」クラスは共通した性質を持つ部分もあるが,それぞれ異なる性質を持つ部分も存在する.このように,共通した部分を共有しながら,違っているところだけを定義しなおすことで,新しいクラスを定義するのが,継承という方法である.継承を用いたプログラミング方法を,差分プログラミングと呼ぶ.

　以上に挙げたような特徴を有効に活用することで,より効率的でミスの少ない,理解しやすいプログラミングが可能となる.Rubyは,このオブジェクト指向という考えかたを徹底して導入したプログラミング言語である.

　Rubyは,処理の細部は言語に任せて人間は問題の本質に集中できるよう,開発効率を向上させるように設計されている.その一方で,プログラムを実行する際の実行速度は,インタプリタであるという要因もあり,Ruby単体で数値計算を行うには非常に遅い.そこで,C言語,もしくはC++によって拡張ライブラリをプログラミングし,Rubyに対して静的,ないし動的に組み込むことで,Rubyの最大の欠点ともいえる実行速度の遅さを克服することが可能となる.拡張ライブラリを作成するに当たって,RubyにはC言語用のAPI(Application Programming Interface)が用意されており,C言語で記述された関数を呼び出したり,CからRubyの機能を呼び出したりする事を容易にしている.Rubyインタプリタ自体もコアとなる部分以外はこのC言語APIを用いて記述されている.この拡張機能を使うことで,Cから使える,すなわちCやC++,FORTRANで記述された既存のライブラリをRubyからアクセスできる様にして,柔軟かつ高速なアプリケーションを作成することが可能となる.

　拙作「NumRu/fft」ライブラリも,C言語で記述し,高速フーリエ変換のルーチン自体は既存のライブラリである,FFTWおよびISPACK(予定)を利用している.

　NumRu/fft ライブラリ(以下,本ライブラリ)は, C言語,あるいはFORTRANで記述された既存のライブラリを利用して実際の計算を行なう, ラッパーライブラリである.現在対応しているライブラリは,FFTW ライブラリである.今後, ISPACKに含まれる FTPACK ライブラリにも対応する予定である.本ライブラリをインストールする前に,これらのライブラリをインストールしておく必要がある.

　FFTW^[11]は,"Fastest Fourier Transform in the West."の頭文字からとられた名前であることが象徴する様に,非常に優れた高速フーリエ変換ライブラリである.FFTWライブラリ自体は,C言語で記述されている.可搬性にも考慮がなされており,Rubyとほぼ同程度にあらゆるOSで使用する事ができる.但し,FFTWにはコサイン変換,サイン変換が存在しない.

　ISPACK^[14]は,「主に簡単な流体方程式の数値計算に必要となる基本的な道具(スペクトル変換, 時間積分, IO, 等)をサブルーチン群としてまとめたもの」(石岡(2000)より引用)である.この中に含まれているFTPACKを使用する.ISPACKは,主にベクトル計算機上で使用されることを念頭においた設計となっている.しかし,個人利用の範囲内でも十分に高速である.

　FFTに対するRuby側の入出力として,NArrayクラスを採用している.田中(2000-2001)^[9]によるとNArrayパッケージは,「多次元数値配列クラスです. 1,2,4 byte 整数,単/倍 精度 実数/複素数,およびRubyオブジェクトを要素に持つことができます.これによりRubyでも大量の数値を扱う計算が,簡単かつ高速にできるようになります.」とある.Ruby本体にも配列は存在し,多次元配列を構成する事は可能だが,データの要素一つ一つをオブジェクトとして構造体に包んでしまうため,演算の速度は著しく遅くなる.これを回避した仕様となっているのが,NArrayクラスである.

　これらのライブラリの仲立ちをし,Ruby上で使用できるようにしたものが,拙作「NumRu/fft」ライブラリである.本ライブラリはデータを整形して高速フーリエ変換ライブラリにデータを渡し,出力を再びRubyで扱えるものに整形しなおすというものであるので,実行速度は高速フーリエ変換ライブラリにほとんど依存している.

　本ライブラリは,以下の8つのクラスメソッドを提供する.

• fft　(複素フーリエ正変換)
• ffti　(複素フーリエ逆変換)
• rfft　(実フーリエ正変換)
• rffti　(実フーリエ逆変換)
• cosfft　(フーリエコサイン正変換)
• cosffti　(フーリエコサイン逆変換)
• sinfft　(フーリエサイン正変換)
• sinffti　(フーリエサイン逆変換)

但し,このうち現在使用可能なメソッドは fft, ffti の二つである.

　インストール方法を述べる.本ライブラリは,Ruby拡張ライブラリの規則に従って作成されているため,環境に依存しない,容易なインストールが可能である.

1. NumRu/fft パッケージをダウンロードし,任意のディレクトリに展開する.
   # tar xzvf numru_fft-0.0.2a.tar.gz
2. 展開してできたディレクトリへ移動する.
   # cd numru_fft-0.0.2a/
3. extconf.rb スクリプトを実行する.
   # ruby extconf.rb
4. make コマンドを実行する.
   # make
5. make install コマンドを実行する.
   # make install

　現在のバージョンでは,NArray#fft(),NArray#ffti()で実行する事が可能である.しかし,次回リリースでは,fftの一連のメソッドはNumRuモジュールのモジュールメソッドになる予定である.

　参考として,以下本ライブラリに添付しているテストスクリプトの全文を示す.

require "narray"

if File.exist?("./fft.so")
  require "fft"
else
  require "numru/fft"
end

na=NArray.scomplex(100,100,100)
na[2,0..99,0..99]=1.0
na=na.fft(0)
na=na.fft(1)
na=na.fft(2)

na.ffti

nb=NArray.dcomplex(100,100,100)
nb[10,0..99,0..99]=1.0
nb=nb.fft(0,2)
nb=nb.fft(1)
nb.ffti(-1)

print "ok.\n"

　本ライブラリは,以下の環境で製作,動作確認をしている.

Ruby 1.6.5 (2001-10-05) [i386-linux]
gcc version 2.95.2 20000220 (Debian GNU/Linux)
Debian GNU/Linux 2.2 (potato)

　本ライブラリは,未だ開発の途上であり,さらなる拡張の余地を残している.現在のバージョンでは,FFTWライブラリの複素フーリエ正変換(FFTWの内部関数名 fftw),および逆変換(fftwb)に対応しているのみで,実数正変換,および逆変換には対応しておらず,ISPACKについては完全に未実装である.

　今後の予定としては,以下のようになっている.

• ISPACKライブラリを利用できるようにし,すべてのメソッドを利用可能にする.
• 完全に利用できるようになったあかつきには,NArray パッケージに patch を送り本ライブラリを融合する.
• 細かなバグフィックスとパッケージの維持を心がける.

　次回リリースでは,ISPACKによるサイン変換,コサイン変換を組みこむこと,NArrayライブラリに対するパッチの形式でリリースすることの二点を目指して開発を続けて行きたい.