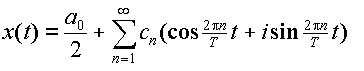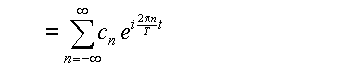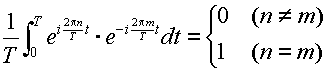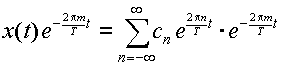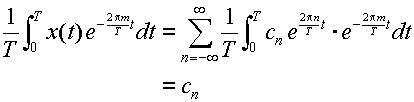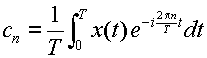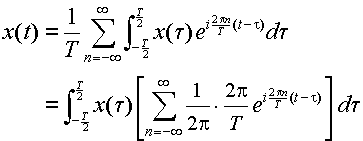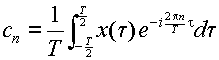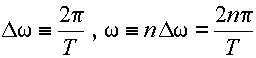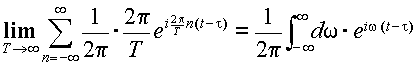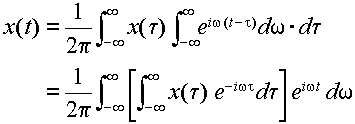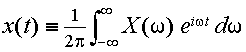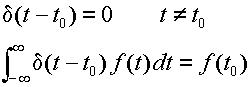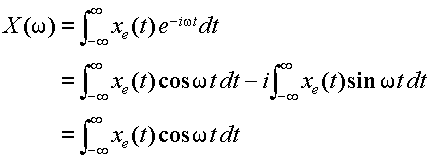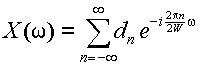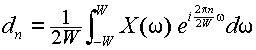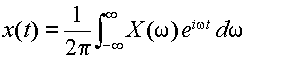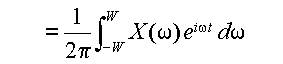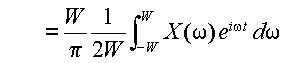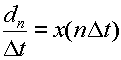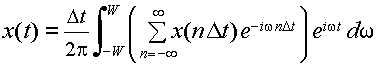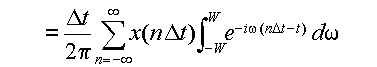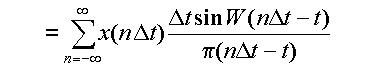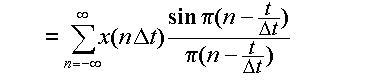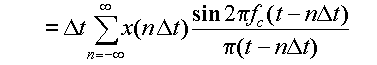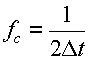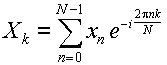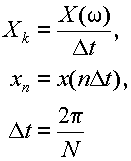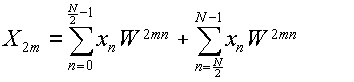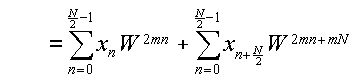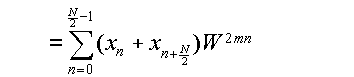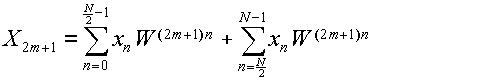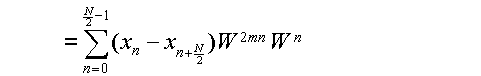フーリエ級数(
Fourier Series)は, 有限区間 0≦t≦T
で定義された関数,あるいは周期がTの周期関数を次のように正弦級数と余弦級数で展開して表わしたものとして定義される。
 |
(3.1.1) |
この式が成り立つための条件は,x(t)
がたかだか有限個の有限な不連続点しか持たず,また,あっても有限個の極値,極大値,
または極小値を持つことである.これを,ディリクレの条件と言う.
(3.1.1)式は, 係数 an 及び bn
を以下のようにおきかえる事で,より簡単な形で表わす事ができる.
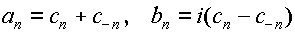 |
(3.1.2) |
を代入すると,
となる.ただし,
 |
(3.1.4) |
とした.
次の式は,直交関係の式として有名であり、容易に証明できる.
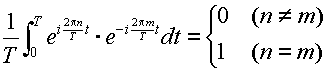 |
(3.1.5)
|
式(3.1.5)の両辺に
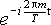
をかけて式(3.1.7)を用いると,
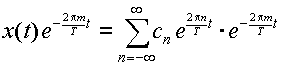 |
(3.1.6) |
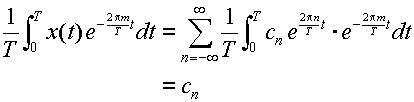 |
(3.1.7) |
よって,
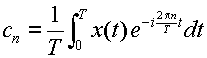 |
(3.1.8) |
を得る.式(3.1.2)を用いて書き換えれば,
 |
(3.1.9a) |
 |
(3.1.9b) |
を得る.
前節に示したフーリエ級数は,有限区間[0,T]で定義された関数,もしくは周期Tの周期関数についてのみ適用する事ができる.ここでは,より一般的な関数,非周期的関数にまでフーリエ級数を拡張する.この拡張は,非周期的関数の周期は,T→∞の極限を考えることで実現できる.
前節では有限区間を [0,T] としたが,ここでは [-T/2,T/2] ととる.この時のフーリエ級数は次のように与えられる.
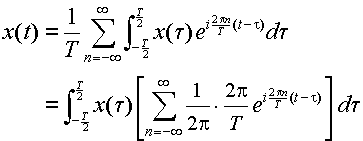 |
(3.2.1) |
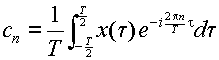 |
(3.2.2) |
式(3.2.2)を式(3.2.1)に代入すると,
 |
|
 |
(3.2.3) |
T→∞とし,
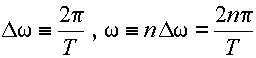 |
(3.2.4) |
とおくと,[ ]
で囲んだ部分について積分におきかえる事ができる.
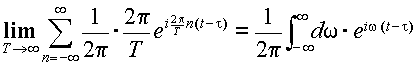 |
(3.2.5) |
よって,
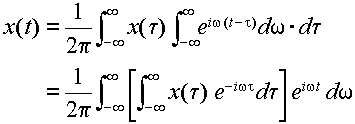 |
(3.2.6) |
ここで,式(3.2.6)の [ ] の部分を
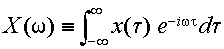 |
(3.2.7) |
とした時,このX(ω)を
x(t) のフーリエ変換と呼ぶ.また,式(3.2.6)をX(ω)で表わすと,
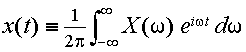 |
(3.2.8) |
となり,これは
フーリエ逆変換を表わしている.
次に,インパルス関数に対するフーリエ変換について議論する.
ここでは,インパルス関数を次のようなある関数に対して数値
f (x) を割り当てるような超関数として定義する.
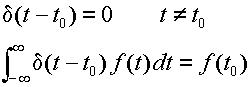 |
(3.2.9) |
この関数は,ディラック(Dirac)のδ関数と呼ばれる.このインパルス関数δ(t)
に対してフーリエ積分を行なう. ここで t
0=0
としても一般性を失わないので,
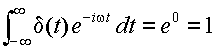 |
(3.2.10) |
を得る.
式(3.2.7)のx(t)が実数関数であり,偶関数,もしくは奇関数であった場合,フーリエ変換は特別な形に書きかえる事ができる.まずは,x(t)が偶関数である場合を考える.偶関数をxe(t)と表わす.このとき,フーリエ変換公式,式(3.2.7)は次のように書きかえられる.
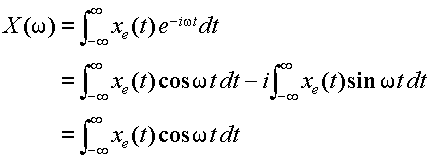 |
(3.3.1) |
式(3.3.1)の2行目第2項は,非積分関数は奇関数となるので0に等しい事を用いた.この形で表わしたものを,フーリエコサイン変換と呼ぶ.このときのX(ω)もまた,X(-ω)を計算することで偶関数であることが容易に導出できる.
次に,x(t)が奇関数である場合を考える.先ほどと同様に奇関数をxo(t)と表わす.同様にして式(3.2.7)を書きかえると,
 |
(3.3.2) |
となり,X(ω)は純虚数の関数として表わされる.このX(ω)に含まれる虚数iを外に出した形で書きなおした
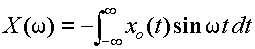 |
(3.3.3) |
を,フーリエサイン変換と呼ぶ.これもコサイン変換同様,X(-ω)を計算すると,-X(ω)になり,奇関数である事がわかる.
この節では,先に述べた連続的な関数のフーリエ変換を,計算機上で行なうことを可能にする為に適当な修正を行なう.
すなわち,連続な関数を離散的な数列に変換する「標本化(sampling)」と,定義域を有限にする「局所化」である.
ある関数 x (t) のフーリエ変換 X(ω)
が局所的であるとする.すなわち,あるWに対して
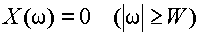 |
(3.4.1) |
を満足していると仮定すると,フーリエ級数は次のように計算できる.
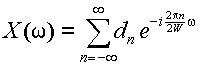 |
(3.4.2) |
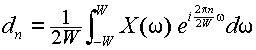 |
(3.4.3) |
式(3.4.2)では,式(3.2.7)とは異なり,
i の代わりに-
i
とおいた.フーリエ変換の逆変換の式,式(3.2.8)
と書ける.式(3.4.1)の条件より,積分区間は-∞から∞までと,-WからWまででは積分の結果は同じと考えてよい.式(3.4.4)において,
π/W=Δt とし, t を nΔt とおくと,
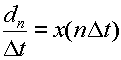 |
(3.4.5) |
となる.これを式(3.4.2)に代入すると
 |
(3.4.6) |
となる.この式はX(ω)のフーリエ係数d
nがx(t)を間隔Δtごとにサンプルした標本値系列
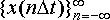
であることを示している.
再びフーリエ逆変換の式,式(3.2.8)を用いると,
となる.これは,間隔Δtごとに標本化したx(t)の値
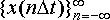
から,もとの関数 x(t) を再現できることを示している.ここで,
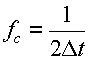 |
(3.4.8) |
と表わした.このf
cは,「
ナイキストの標本化周波数(Nyquist
sampling rate)」(あるいは単にナイキスト周波数)と言う.もし間隔Δtで標本化した連続関数
x(t) の周波数帯域がf
cより小さい周波数に限られていたなら,関数
x(t) は標本 x
n
から完全に再現されうる.逆に,帯域幅がナイキスト周波数を越えてしまうような連続関数を標本化する時には,
-f
c < f < f
cの範囲外のフーリエ変換の結果が帯域幅の内側にひずみとして現れてしまう.この現象を
エイリアシング(aliasing, または折り返しひずみ)という.
ここでは,はじめに周波数領域の関数X(ω)が限られている(局所的である)と仮定したが,逆に時間領域の関数x(t)が有限区間で定義されている(局所的である)とした場合でも,同様の結果が得られる.即ち,周波数を局所的にすれば時間に離散化とサンプリング定理が適用され,時間を局所的にすれば周波数に離散化とサンプリング定理が適用される.
離散フーリエ変換を計算するにはN2回の乗算が必要であり,
N が大きくなると計算に必要な時間は急速に増大する.ところが,1965年にクーリーとチューキーによって提案された高速フーリエ変換(Fast Fourier Transform, 略して FFT)のアルゴリズムは,これを最小で N logN回にまで減らす.この節では,FFTの数学的側面を簡単に述べる.
式(3.4.6)は,次のように書きかえる事ができる.
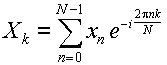 |
(3.5.1) |
これは,
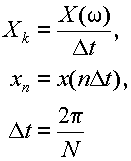 |
(3.5.2) |
としたものである.式(3.5.1)はさらに書きかえる事ができて,
 |
(3.5.3) |
とできる.
Nが偶数である場合を考える.k=2m,即ちXkの偶数番目の成分に注目したとき,
WN=1である事を利用して,
と表わせる.この時,
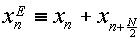 |
(3.5.5) |
とおくなら,式(3.5.4)は,X
2m(m=0,…,N/2-1)が長さN/2の数列
x
Enのフーリエ変換となる事を表わしている.
同様にして,k=2m+1,即ちXkの奇数番目の成分に注目したとき,WN/2=
-1となる事を利用して,
と表わす事ができる.式(3.5.5)同様,
 |
(3.5.7) |
とおくと,式(3.5.6)はX
2m+1(m=0,…,N/2-1)が長さN/2の数列
x
Onのフーリエ変換となる事を表わしている.
この分割を,2で割り切れる段階まで進めることで計算回数を減らしていく事ができる.N=2Mで表わせる場合が最も効率良く,あるひとつのXについての和の計算がlogN=M回,数列Xすべてについては,NlogN回の計算で結果を得る事ができる.以上が高速フーリエ変換のアルゴリズムである.